Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 합집합
- null # undefined
- 조지 불
- 딥러닝
- 입출력
- pop()
- Python
- 성적 입력받기
- 리스트와 차이점
- false
- 정보를 담을 수 있는 그릇
- Java Script # == # === # difference # 차이
- 불리안
- index()
- 차집합
- 그룹 # 그룹 해체 # 단축키 #figma #Figma
- input()
- 귀도 반 로섬
- 부스트캠프
- 변할 수 있는
- 변수와 입출력
- insert()
- 조건문 큰 수부터 입력받아야하는 이유
- html
- 변수
- 파이썬
- 1일차
- a=1
- append()
- del()
Archives
- Today
- Total
I about me
[중간고사] 2-(2). Divide and Conquer - Matrix Multiplication 본문
Algorithm/Lecture note
[중간고사] 2-(2). Divide and Conquer - Matrix Multiplication
ssungni 2024. 4. 24. 02:011. Iterative Algorithm
- C = AB, (이때, n * m 크기의 행렬 A, m * p 크기의 행렬 B → n * p의 크기의 행렬 C)


- 시간복잡도
- 위의 알고리즘은 Θ(npm)의 시간 복잡도를 가짐.
즉, 일반적으로 Θ(n^3)의 시간 복잡도를 가짐. (for문 3개인 거 확인 가능)
- 위의 알고리즘은 Θ(npm)의 시간 복잡도를 가짐.
2. Divide and conquer Algorithm (Brute force)
- 2^n의 크기를 가지는 동일한 행렬 A, B에 대해 수식은 다음과 같음.
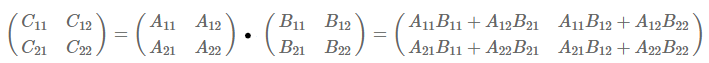

- 다음에 따라 8번의 곱셈과 4번의 덧셈이 필요하다는 것을 알 수 있음.
즉, 8개의 n/2 크기의 부분 행렬의 곱과 그들의 합 Θ(n^2) 으로 이뤄질 수 있음. - 시간복잡도
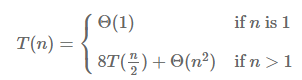


- 위 수식으로 풀면, Θ(n^3)의 시간 복잡도를 가지며,
Iterative 알고리즘과 동일한 시간 복잡도를 가진다는 것을 알 수 있음.
3. Strassen Algorithm ( 슈트라센 )
| (1) X, Y, Z 설정 | (2) M 계산 (7번 곱셈 + 18번의 덧셈) | (3) Z의 I, J, K, L 계산 |
 |
 |
 |
- 시간복잡도

- 곱셈을 더 적게 하는 것은? 슈트라센
- 그러므로 2 * 2 행렬곱에서 best임!!!
'Algorithm > Lecture note' 카테고리의 다른 글
| [중간고사] Ram access model - 메모리는 임의 접근을 한다! (0) | 2024.04.24 |
|---|---|
| [중간고사] 2-(4). Divide and Conquer - Uneven Split, Selection Problem (0) | 2024.04.24 |
| [중간고사] 1. Algorithm Efficiency (0) | 2024.04.22 |
| 2-(1). Induction Proof & Recurrence Relation (0) | 2024.04.22 |
| [중간고사] 2-(5). Divide and Conquer - Selection Problem (0) | 2024.04.20 |





