Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
Tags
- append()
- index()
- 변수
- Java Script # == # === # difference # 차이
- 조건문 큰 수부터 입력받아야하는 이유
- input()
- html
- 조지 불
- Python
- 합집합
- 변할 수 있는
- a=1
- 파이썬
- null # undefined
- del()
- 성적 입력받기
- 귀도 반 로섬
- prompt
- langchain
- 변수와 입출력
- 부스트캠프
- 딥러닝
- 입출력
- insert()
- 그룹 # 그룹 해체 # 단축키 #figma #Figma
- 리스트와 차이점
- 불리안
- 정보를 담을 수 있는 그릇
- pop()
- 차집합
Archives
- Today
- Total
I about me
[중간고사] 1. Algorithm Efficiency 본문
예상문제 - Ram model 개념
알고리즘 분석의 가장 중요한 도구는
1) RAM 계산 모델
2) 최악의 경우(worst-case)의 점근적 분석(asymptotic analysis)
Ram model
- 알고리즘은 컴퓨터 과학의 중요하고 지속적인 부분임
왜냐하면 기계-독립적인 알고리즘 방식으로 연구할 수 있기 때문 - 이것은 모든 분석에 RAM 모델의 계산을 사용하기 때문
* RAM: Random Access Machine - 알고리즘 실행 시간: RAM 모델에서의 단계 수를 세어 측정함
- 각 단계의 정확한 시간은 다르지만, RAM은 그 모든 것을 동등하다고 가정
- 각 "간단한" 작업(+, *, -, =, if, call)은 한 번의 1단계 소요
- 루프 서브루틴은 간단한 작업이 아님
이들은 데이터의 크기와 서브루틴의 내용에 따라 달라짐- 예를 들면, "정렬"은 단일 단계 작업이 아님
- 각 메모리 접근은 한 번의 1단계 소요(캐시나 디스크 상에서)
- 게다가, 우리는 필요한만큼의 메모리를 가지고 있음
예상문제 - 계산 문제
Best-Case/Average-Case/Worst-Case Time Complexity

- 최악의 경우(worst-case) : 크기 n인 모든 사례에 대한 단계의 최대 개수 --> 실제에서 가장 유용
- 최선의 경우(best-case) : 크기 n인 모든 사례에 대한 단계의 최소 개수
- 평균의 경우(average-case) : 크기 n인 모든 사례에 대한 단계의 평균 개수
Asymptotic Notations(빅오, 세타, 오메가)
 |
 |
 |
| Upper Bound | Tight bound | Lower bound |
| 연산 ↑ : worst-case | average-case | 연산 ↓ : best-case |
| O [빅오] | θ [세타] | Ω [오메가] |
| f(n) ≤ c · g(n) | c2·g(n) ≤ f(n) ≤ c1·g(n) | f(n) ≥ c · g(n) |
예상문제 - 간단한 코드가 주어졌을 때 시간 복잡도 분석(O, θ 구분하)
교재 예시 1. Selection Sort
selection_sort(int s[], int n) {
int i, j;
int min;
for (i = 0; i < n; i++) {
min = i;
for (int j = i + 1; j< n; j++)
if (s[j] < s[min]) min = j;
swap(&s[i], &s[min]);
}
}최선, 평균, 최악의 경우에 모두 n^2에 비례하는 시간을 소비하므로 Θ(n^2)이다.
교재 예시 2. Insertion Sort
for (i = 1; i < n; i++) {
j = i;
while ((j > 0) && (s[j] < s[j - 1])) {
swap(&s[j], &s[j - 1]);
j = j - 1;
}
}- Insertion Sort는 왜 빅오로 사용해야하며, θ를 사용하지 않는 이유는 무엇인가요?
- 최선의 경우 Ω(n), 평균의 경우 θ(n^2), 최악의 경우 O(n^2) 이므로 θ를 사용하지 않고 O를 사용해야한다.
교재 예시 3. String Pattern Match
int findmatch(char *p, char *t)
{
int i, j; /* counters */
int m, n; /* string lengths */
m = strlen(p)
n = strlen(t)
for(i = 0; i<=(n-m); i=i+1) {
j = 0
while((j<m) && (t[i+j] == p[j]))
j = j + 1;
if (j == m) return i;
}
}- 주어진 코드는 문자열 t에서 문자열 p의 첫 번째 출현을 찾는 함수
- for 루프는 n-m+1번 반복됨. (n은 t의 길이, m은 p의 길이)
- while 루프는 최악의 경우에 m번 반복됨.
- 그러므로 O(nm)임
교재 예시 4. Matrix Multiplication
for (i=1; i<=x; i++)
for (j=1; j<=y; j++) {
C[i][j] = 0;
for (k=1; k<=z; k++)
C[i][j] += A[i][k] * [k][j];
}- 첫 번째 for문에서 x번, 두 번째 for문에서 y번, 세 번째 for문에서 z번 → O(xyz)
교재 예시 4. Matrix Multiplication
function pesky(n)
r:=0
for i:=1 to n do
for j:=1 to i do
for k:=j to i+j do
r:=r+1
return(r)++
예상문제 - Dominace 관계
Dominance는 말 그대로 누가 왕인가?

- 기본적인 비교군 (루트 n은 어디에 들어가는가?)
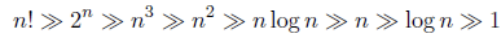
- Advanced Dominance Rankings
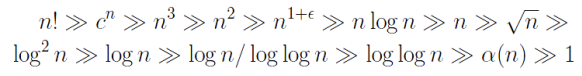
- logarithm: 1이 될 때까지 N을 몇 번 곱해야하는가?
- ex)
8 / 2 / 2 / 2 = 1
8이 1이 될 때까지 2를 세 번 나눠야 하므로 log₂8 = 3이다.
- ex)
'Algorithm > Lecture note' 카테고리의 다른 글
| [중간고사] Ram access model - 메모리는 임의 접근을 한다! (0) | 2024.04.24 |
|---|---|
| [중간고사] 2-(4). Divide and Conquer - Uneven Split, Selection Problem (0) | 2024.04.24 |
| [중간고사] 2-(2). Divide and Conquer - Matrix Multiplication (0) | 2024.04.24 |
| 2-(1). Induction Proof & Recurrence Relation (0) | 2024.04.22 |
| [중간고사] 2-(5). Divide and Conquer - Selection Problem (0) | 2024.04.20 |




