Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- Java Script # == # === # difference # 차이
- a=1
- false
- 리스트와 차이점
- input()
- append()
- 정보를 담을 수 있는 그릇
- Python
- 불리안
- html
- index()
- 1일차
- 합집합
- 성적 입력받기
- pop()
- 변수
- 귀도 반 로섬
- 차집합
- 조건문 큰 수부터 입력받아야하는 이유
- 딥러닝
- 변할 수 있는
- 파이썬
- 입출력
- 부스트캠프
- insert()
- null # undefined
- 변수와 입출력
- del()
- 그룹 # 그룹 해체 # 단축키 #figma #Figma
- 조지 불
Archives
- Today
- Total
I about me
[Deep learning] Gradient Descent 본문
본 글은 https://iai.postech.ac.kr/teaching/deep-learning/ 해당 페이지를 보고 공부한 것을 정리한 내용입니다
Gradient Descent
- 이번 강의에서는 경사 하강법 알고리즘과 그 변형들에 대해 다룰 것
- Batch Gradient Descent (배치 경사 하강법)
- Stochastic Gradient Descent (확률적 경사 하강법)
- Mini-batch Gradient Descent (미니 배치 경사 하강법)
- 세 가지 경사 하강법 알고리즘의 개념을 로지스틱 회귀 모델을 사용하여 탐구할 것
- Gradient Descent의 한계
- Adaptive learning rate
- 학습률이 너무 크다면? 모델이 최적의 값을 지나치게 되어 수렴하지 않을 수 있다
- 학습률이 너무 작다면? 학습이 너무 느려져 시간이 많이 걸릴 수 있다.
- Adaptive learning rate
Batch Gradient Descent (= Gradient Descent)
- Repeat : x ← x − α∇xf(x) for some step size α>0
- 반복하는데, 어떻게?
- x를 x에서 α 곱하기 x에 대한 f의 기울기(그래디언트)를 뺀 값으로 갱신
- 는 학습률 또는 스텝 크기로, 0보다 큰 값이어야함
- 반복하는데, 어떻게?
- 손실 함수(E(w)): 모든 훈련 예제에 대한 평균 손실 함수

- ℓ : 손실, 번째 예제에 대한 예측값 𝑦^𝑖와 실제값 𝑦𝑖 사이의 손실(loss)
- m은 훈련 데이터의 총 개수로 난눠 평균을 하게 해줌
- 는 파라미터 𝜔를 사용하여 입력 𝑥𝑖에 대한 모델의 예측값
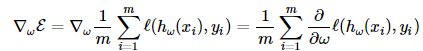
- 위 수식은 손실 함수에 그래디언트를 구한 것으로 이 그래디언트를 사용하여 파라미터 𝜔를 업데이트할 수 있음
그리하여,
- ℓ : 손실, 번째 예제에 대한 예측값 𝑦^𝑖와 실제값 𝑦𝑖 사이의 손실(loss)
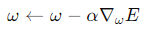
| 장점 |
|
| 단점 |
|
Stochastic Gradient Descent (SGD)
- 무작위로 선택된 단일 훈련 예제의 기울기를 기반으로 파라미터를 업데이트
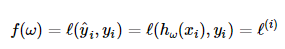
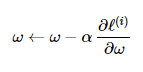
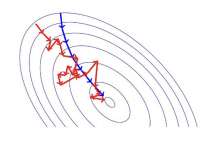
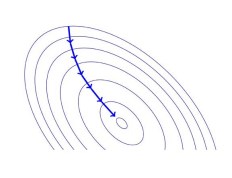
- SGD는 소음이 있는 방향으로 이동하지만, 평균적으로는 내리막 방향으로 이동함
- 수학적 정당성: 훈련 예제를 무작위로 샘플링하면, 확률적 기울기는 배치 기울기의 편향 없는 추정치가 됨.
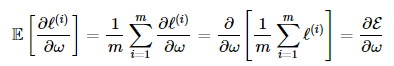
- SGD는 때때로 더 낫다.
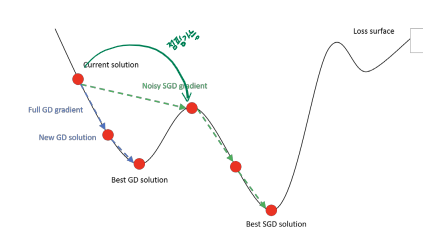
- noisy이 있는 SGD 기울기는 때때로 지역 최적값을 탈출하는 데 도움이 될 수 있음
- 이것이 항상 일어난다고 보장할 수는 없음
Mini-Batch Gradient Descent
- SGD의 잠재적인 문제점: 기울기 추정치가 매우 noisy함.
- 타협 방안: 중간 크기의 훈련 예제 집합 (<m)에서 기울기를 계산 → 이때, 집합을 mini-batch라고 함.

- 큰 미니 배치에서 계산된 확률적 기울기는 분산이 작음
- 많은 예제를 포함하는 미니 배치를 사용하면 기울기 추정치가 더 안정적이고 노이즈가 적은 경향 O
- 미니 배치 크기 𝑠는 설정해야 하는 하이퍼파라미터
- 큰 미니 배치에서 계산된 확률적 기울기는 분산이 작음
| 장점 |
|
| 단점 |
|
Limitation of the Gradient Descent
Setting the Learning Rate
- 학습률은 어떻게 setting하는가? // 경시 하강법의 한계: 학습률 설정의 어려움
- 작은 학습률은 느리게 수렴하고 잘못된 지역 최솟값에 갇힐 수 있음
- 큰 학습률은 overshooting하여 불안정해지고 발산할 수 있음
// 학습률 설정하는 방법
- 아이디어 1)
- 다양한 학습률을 시도해보고 "딱 맞는" 값을 찾음
- SGD Learning Rate (= Step Size) 가정
- 경사 하강법은 스텝 크기를 고정하기 위해 "국소 곡률(local curvature)"의 크기에 대해 강한 가정을 하며
- 모든 방향에서 동일한 스텝 크기가 의미가 있다는 등방성(isotropy)에 대해서도 가정을 함.

- 아이디어 2) Adaptive Learning Rate
- 더 똑똑한 방법을 사용 → 지형에 "적응"하는 적응형 학습률을 설계
- 공간적(Spatial) 및 시간적(Temporal) 적응.
- SGD Learning Rate : Spatial
- 모든 특징(feature)에 동일한 학습률을 할당함
- 데이터의 기울기가 균일하게 분포되어 있는 경우

- 데이터의 기울기가 방향에 따라 다르게 분포되어 있는 경우
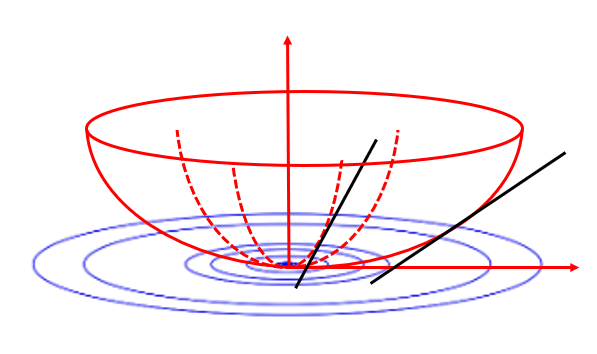
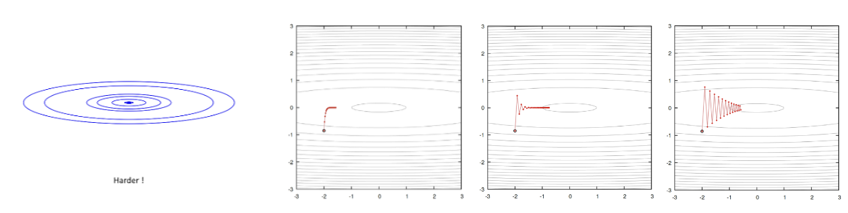
- 데이터의 기울기가 균일하게 분포되어 있는 경우
- 모든 특징(feature)에 동일한 학습률을 할당함
- SGD Learning Rate : Temporal
- 전략
- 훈련 초기에 큰 학습률을 사용하여 최적점에 가깝게 근접하는 전략
- 학습률을 점차적으로 감소시켜 변동을 줄여 안정성을 높이는 전략
- 구체적인 전략
- SGD
- ω 는 가중치, 𝛼는 학습률, 𝑔는 그래디언트

- ω 는 가중치, 𝛼는 학습률, 𝑔는 그래디언트
- Adagrad
- 는 각 시점까지의 그래디언트의 제곱 합 → 나누어지니까 학습률이 점점 작아질 거임
- 은 0으로 나누는 것을 방지하기 위한 작은 값

- SGD
- 전략
'AI > Deep Learning' 카테고리의 다른 글
| [Deep learning] DP → Backpropagation (0) | 2024.06.25 |
|---|---|
| [Deep learning] Perceptron (0) | 2024.06.25 |
| [Deep learning] Overfitting (0) | 2024.05.30 |
| [Deep learning] Machine Learning (0) | 2024.05.30 |
| [Deep learning] Optimization (0) | 2024.05.02 |




