Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 파이썬
- 변할 수 있는
- 부스트캠프
- Java Script # == # === # difference # 차이
- null # undefined
- 불리안
- insert()
- 성적 입력받기
- 귀도 반 로섬
- 변수와 입출력
- html
- false
- pop()
- 딥러닝
- Python
- 합집합
- 변수
- input()
- 조건문 큰 수부터 입력받아야하는 이유
- 조지 불
- 입출력
- append()
- a=1
- 정보를 담을 수 있는 그릇
- 차집합
- del()
- 리스트와 차이점
- index()
- 그룹 # 그룹 해체 # 단축키 #figma #Figma
- 1일차
Archives
- Today
- Total
I about me
[중간고사] 4. Dynamic Programming 본문
예상문제 1. Divide and Conquer과 Dynamic Programming의 차이점을 서술하시오.
| Divide and Conquer | Dynamic Programming | |
| 공통점 | 큰 문제를 작게 | 큰 문제를 작게 |
| 차이점 | - Top-down 접근 방식 - 상호 관련이 없는 경우에 효율적 근데 관련 있으면 비효율적 |
- Bottom-up - 재 컴퓨팅 xx -> 저장 + look it up 그러니까 관련 있는 거할 때 효율적 |
| 예시 | Merge Sort, Quick Sort | Longest Common Subsequence, Matrix Chain Multiplication |
예상문제 2. LCS(Longest Common Subsequence)
시간복잡도: O(mn)
- 여기서 m과 n은 각각 두 문자열의 길이를 나타냄
- 두 문자열의 길이에 비례하여 작동하기 때문에, 문자열의 길이가 증가할수록 연산량도 증가

LCS Pseudo Code
LCS[0][] = 0
LCS[][0] = 0
Start from LCS[1][1]
Compare X[i] and Y[j]
If X[i] = Y[j] # 같으면
LCS[i][j] = LCS[i-1, j-1] + 1 # 역슬래쉬 + 1
Point an arrow to LCS[i][j] # 내 자리 저장
Else # 다르면
LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1]) # 왼쪽 옆과 위 중 큰 수로
Point an arrow to max(LCS[i-1][j], LCS[i][j-1]) # 그 친구의 시초를 찾는 거임
LCS Back Pointer Sudo Code
i <- n, j <-m
while Mij > 0
print Bij
(i, j) <- Bij - (1, 1)
Example
#1. Determine an LCS of <T, H, O, R, N, Y> and <E, N, T, R, O, P, Y>

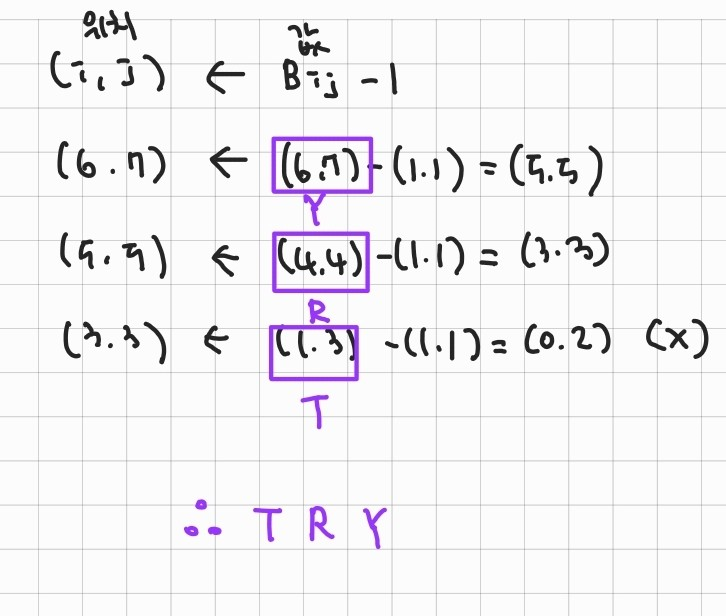
Example
#2. Determine an LCS of <1, 0, 0, 1, 0, 1, 0, 1> and <0, 1, 0, 1, 1, 0, 1, 1, 0>

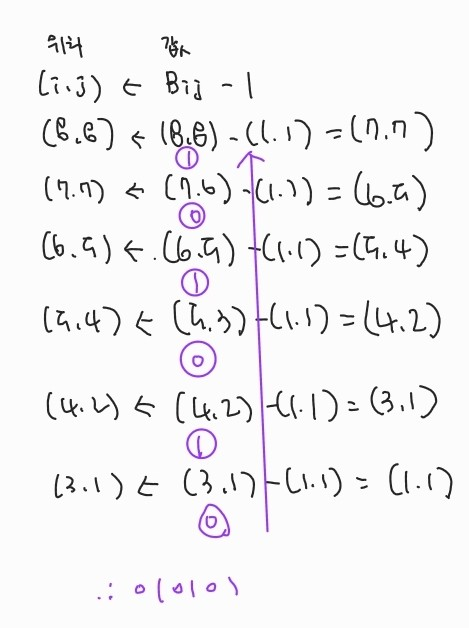
더보기
| LCS "M" part | LCS "B" part |
| 같아? 역슬(래시) + 1 | 내 위치 저장 |
| 달라? 위 옆 중 큰놈 | 큰놈의 위치를 저장 (옆 위치 or 위 위치) |
| 두 값이 같을 때 (옆 위치) |
최종 답 구하기!
위치 ← 값 - (1, 1)
(i, j) ← Bij - (1, 1)
'Algorithm > Lecture note' 카테고리의 다른 글
| [기말고사] 6-(1). 그래프 종류 (0) | 2024.06.05 |
|---|---|
| [기말고사] 5. Heap and Greedy Approach (0) | 2024.06.03 |
| [중간고사] 3-(2). Sorting - Merge Sort (1) | 2024.04.28 |
| [중간고사] 3-(1). Sorting의 개념과 종류 (0) | 2024.04.27 |
| [중간고사] 2-(3). Divide and Conquer - Master Theorem (0) | 2024.04.27 |



