Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 불리안
- false
- 부스트캠프
- 딥러닝
- del()
- insert()
- Python
- 입출력
- html
- 그룹 # 그룹 해체 # 단축키 #figma #Figma
- index()
- 정보를 담을 수 있는 그릇
- null # undefined
- 조건문 큰 수부터 입력받아야하는 이유
- 변할 수 있는
- 리스트와 차이점
- input()
- 변수
- 변수와 입출력
- 1일차
- a=1
- 귀도 반 로섬
- append()
- 파이썬
- 조지 불
- 차집합
- 성적 입력받기
- pop()
- Java Script # == # === # difference # 차이
- 합집합
Archives
- Today
- Total
I about me
[이것이 코딩테스트다] 7. 최단 경로 문제 본문

해당 강의를 참고하여 공부를 진행했습니다.
https://www.youtube.com/watch?v=m-9pAwq1o3w&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC
다익스트라 최단 경로 알고리즘
1. 출발 노드를 설정
2. 최단 거리 테이블을 초기화
3. 방문 x 노드 중에서 최단 거리가 가장 짧은 노드를 선택
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
5. 위 과정 3번과 4번 반복
힙
- heapq.heappush(배열, 넣을 값)
- heapq.heappop(배열)
- O(nlogn)
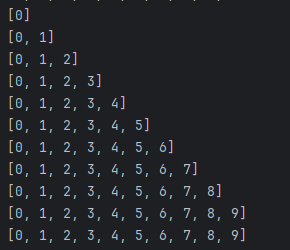
import heapq
def heapsort(iterable):
h = []
result = []
# 모든 원소를 차례대로 힙에 삽입
for value in iterable:
heapq.heappush(h, value)
print(h) # [0, 1, 2, 6, 3, 5, 4, 7, 8, 9]
# 힙에 삽입된 모든 원소를 차례대로 꺼내어 답기
for i in range(len(h)):
result.append(heapq.heappop(h))
print(result)
return result
result = heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
print(result)
힙을 사용하여 구현한 다익스트라 최단 경로 알고리즘
- O(ElogV)

n, m = map(int, input().split()) # 노드, 간선 개수
start = int(input()) # 시작 노드 번호
graph = [[] for i in range(n+1)] # 각 노드에 연결되어 있는 노드에 대한 정보를
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c))
플로이드 워셜 알고리즘
- 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산
- D_ab = min(D_ab, D_ak + D_kb)
- k = 1, k = 2, k = 3 ...
INF = int(1e9)
n = int(input())
m = int(input())
graph = [[INF] * (n + 1) for _ in range(n+1)]
# 자기 자신에서 자기 자신으로 가는 비용은 초기화
for a in range(1, n+1):
for b in range(1, n+1):
if a == b:
graph[a][b] = 0
# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
a, b, c = map(int, input().split())
graph[a][b] = c
# 점화식에 따라 플로이드 위셜 알고리즘을 수행
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
for a in range(1, n+1):
for b in range(1, n+1):
if graph[a][b] == INF:
print('INFINITY', end = " ")
else:
print(graph[a][b], end = " ")
print()
[문제] 전보
import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)
def dijksta(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist:
continue
for i in graph[now]:
cost = dist + i[1]
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
n, m, start = map(int, input().split()) # 노드, 간선 개수
graph = [[] for i in range(n+1)] # 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트 만들기
distance = [INF] * (n+1) # 최단 거리 테이블을 모두 무한으로 초기화
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c))
dijksta(start)
count = 0
max_distance = 0
for d in distance:
if d != 1e9:
count += 1
max_distance = max(max_distance, d)
print(count - 1, max_distance )
[문제] 미래 도시
INF = int(1e9)
n, m = map(int, input().split())
graph = [[INF] * (n + 1) for _ in range(n+1)]
# 자기 자신에서 자기 자신으로 가는 비용은 초기화
for a in range(1, n+1):
for b in range(1, n+1):
if a == b:
graph[a][b] = 0
# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
a, b = map(int, input().split())
graph[a][b] = 1
graph[b][a] = 1
x, k = map(int, input().split())
# 점화식에 따라 플로이드 위셜 알고리즘을 수행
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
distance = graph[1][k] + graph[k][x]
if distance >= INF:
print("-1")
else:
print(distance)
'Algorithm > 이것이 코딩테스트다!' 카테고리의 다른 글
| [이것이 코딩테스트다] 6. DP (1) | 2024.07.24 |
|---|---|
| [이것이 코딩테스트다] 5. 이진 탐색 (1) | 2024.07.22 |
| [이것이 코딩테스트다] 4. 정렬 (0) | 2024.07.19 |
| [이것이 코딩테스트다] 3. DFS/ BFS (0) | 2024.07.18 |
| [이것이 코딩테스트다] 2. 그리디 & 구현 (1) | 2024.07.18 |




